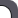для справки:

Что появилось раньше: яйцо или овал?  

Овал, в переводе с французского "единственное число" - ovale, от лат. ovum — яйцо.

Т.е. овал-это фигура яйцеобразной формы, ограниченная кривой линией.

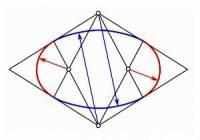
Самым простейшим овалом является окружность у которой расстояния между крайними точками по вертикали и горизонтали - равны.

Как начертить окружность и что она из себя представляет - знают все, поэтому мы даже не будем заострять на ней внимание.

Нас интересуют овалы имеющие некое отличие в размерах между крайними точками по вертикальной и горизонтальной оси.

Такими фигурами являются: овал, овоид и элипс.

Овал

Овал можно построить 2 способами. Первый способ применим когда нам заданы ширина (по горизонтальной оси) и высота (по вертикальной оси) овала.

Второй способ будет интересен если нам будет задана только ширина овала (по горизонтальной оси), а высота его будет неизвестна.

Овоид

Овоид в отличии от овала он имеет только одну ось симметрии.

Радиусы дуг окружностей, центры которых лежат на оси симметрии овоида, не равны друг другу.

Эллипс

Эллипс - замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси,

есть величина постоянная и равная длине большой оси. Хотя эллипс и похож на овал, он таковым не является (на данном сайте он рассмотрен лишь

из-за его похожести на овал). Эллипс относится к лекальным кривым.

Окружность в аксонометрии

Окружность в аксонометрии - также как и эллипс, лишь похожа на овал. Окружность в изометрической проекции будет выглядить

в форме эллипса, но построения будут немного отличаться.

 

Здесь представлен пример как правильно построить ОВАЛ на потолке или декоративной перегородке, с  помощью геометрического построения.
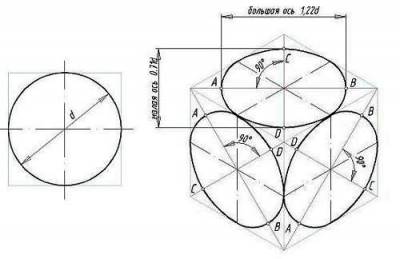
 На рисунках, приведенных ниже, изображена изометрическая проекция куба с окружностями, вписанными в его грани. Квадратные грани куба будут изображаться в в виде ромбов, а окружности в виде эллипсов. Следует запомнить, что малая ось СD каждого эллипса всегда должна быть перпендикулярна большей оси АВ.

2. Находим точки пересечения этой окружности с аксонометрическими осями x и y( n1,n2, n3 и n4 ).

3. Из точек m1 и m2 пересечения вспомогательной окружности с осью z, как из центров радиусом R=m1n4, проводим две дуги n1n2 и n3n4. Пересечение этих дуг с осью z дают тоски C и D.

4. Из центра О радиусом ОС, равным половине малой оси овала, засекаем на большой оси овала точки О1 и О2.

5. Соединяем точки m1 и m2 с точками О1 и О2 и продолжаем прямые до пересечения с дугами n1n2 и n3n4. Обозначаем точки пересечения как 1,2,3 и 4. Эти точки будут являться точками сопряжения большого и малого радиусов овала.

6. Из точек О1 и О2 радиусом R1=О11 проводим две дуги.

Теперь построение окружности в аксонометрии методом овала, считаем законченным.
Таким же образом строятся овалы, расположенные в плоскостях, параллельных плоскостям V и W.

Есть более простой вариант, но требующий аккуратного исполнения: